
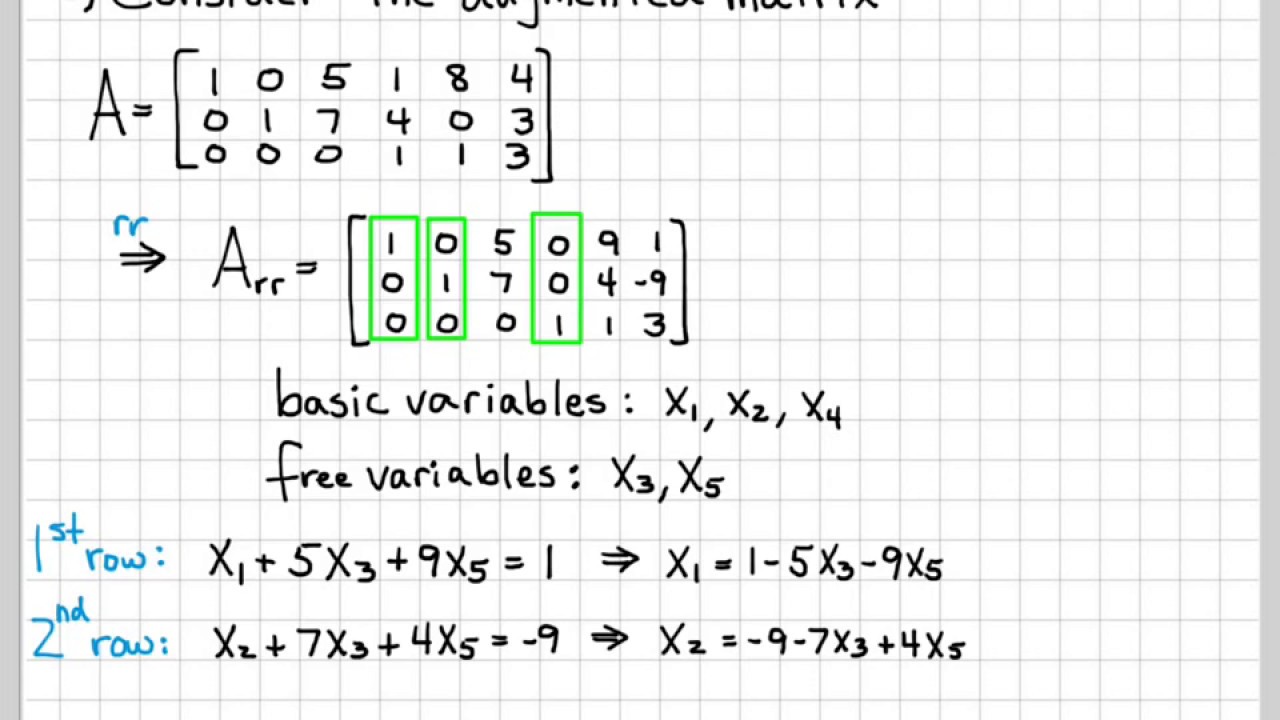
Of the same size before concluding the rank of the matrix. This property could mean that we may need to check multiple different submatrices Taking the determinant of this matrix gives 𝐶 obtained by “deleting” the top row and right However, if we had instead chosen the 2 × 2 submatrix So, we might conclude that R K ( 𝐴 ) ≠ 2 either. “deleting” the bottom row and right column of 𝐴, It is possible to find one 𝑛 × 𝑛 submatrix with aĭeterminant = 0, but another with a determinant
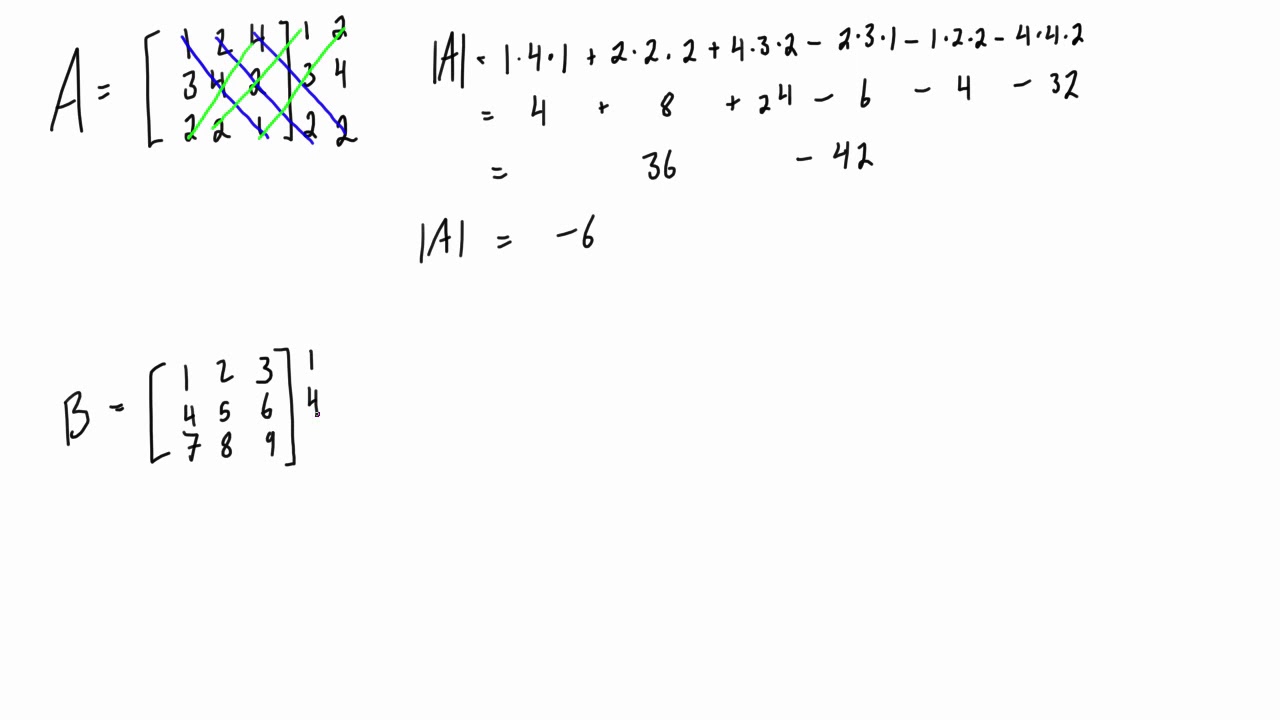
We sometimes need to take care when selecting a submatrix of the original matrix. The determinant of the 3 × 3 matrix is nonzero The largest possible square submatrix of this 3 × 3
Also, since it is not the zero matrix, its rank cannot be 0. Since this is a 3 × 3 matrix, its rank must be betweenĠ and 3. Of rows/columns of the largest square submatrix of 𝐴 Recall that the rank of a matrix 𝐴 is equal to the number
#AUGMENTED MATRIX 3X3 HOW TO#
Let’s look at a simple example of how to find the rank of anotherĮxample 3: Finding the Rank of a Given Matrix 𝐴 for which the determinant is nonzero therefore, The bottom row and right column of 𝐴, let’s call thisĭ e t ( 𝐵 ) = 4 ⋅ 6 − ( − 3 ) ( − 1 ) = 2 0 ≠ 0. The next step is to consider smaller square submatrices, in this case Therefore, by the definition of rank, R K ( 𝐴 ) Submatrix (in this case, 𝐴 itself) is zero. We have found that the determinant of this 3 × 3 The number of rows/columns of the submatrix. If the determinant is nonzero, then the rank of the original matrix is equal to Once we have chosen a submatrix, we can take the determinant of the matrix. Since 𝐴 is already a square matrix, the largest possible square We first need to consider the largest possible square submatrix of 𝐴. Quickly finding the rank of a 3 × 3 matrix is therefore a Particularly due to their occurrence in problems in 3D space. Rows/columns of this submatrix with a nonzero determinant.ģ × 3 matrices are among the most common matrices, The rank of the original matrix is equal to the number of If a submatrix with a nonzero determinant has not been found, repeat stepsġ and 2 for submatrices 1 row and column smaller until a submatrix with a nonzeroĭeterminant is found.If the determinant of the submatrix is zero, repeat step 1 for other possible.The rank of the original matrix is given by the number of rows of the submatrix. Calculate the determinant of this submatrix. Consider the largest possible square submatrix of 𝐴.


 0 kommentar(er)
0 kommentar(er)
